Les statistiques ont pour but de permettre d’objectiver des ressentis, observations, ouï-dire etc., par le recueil de données via un questionnaire standardisé. Leur apport est donc précieux. Cependant, pour bien interpréter les chiffres, il importe d’être attentif à quelques éléments qui peuvent biaiser les résultats si on n’y prend garde.
Nous explicitons donc ici des éléments qui peuvent être utiles pour les AMO dans deux types de situations :
- lorsqu’elles réalisent elles-mêmes des statistiques et qu’il leur faut choisir quels types de données sont les plus pertinentes pour l’objet qu’elles veulent éclairer, donc lorsqu’elles doivent « faire parler » les chiffres ;
- lorsqu’elles collectent des statistiques existantes pour étayer leur diagnostic social, donc lorsqu’il s’agit de « lire et d’interpréter » correctement ces chiffres.
Pour exemplifier le propos, nous nous baserons sur une enquête menée en 2009 par le CAAJ de Huy en collaboration avec le CLPS, portant sur le bien-être des jeunes.
Vaste sujet, qui comporte aussi bien des éléments touchant à la santé qu’à la famille, l’école, etc.
Durant l’année scolaire 2009, un questionnaire a été proposé via internet et via des écoles aux jeunes en âge d’école secondaire.
Le questionnaire comportait trois parties :
- une partie sur le bien-être des jeunes en général : comment se sentent-ils, du point de vue de la forme générale, en famille, à l’école ;
- une partie sur les formes d’aide possibles pour les jeunes en cas de difficultés : vers qui se tournent-ils, connaissent-il des services d’aide et qu’en pensent-ils ;
- une partie portant sur leur consommation en général, avec un volet concernant notamment des produits psychotropes, et d’autres concernant l’usage du GSM et de l’ordinateur.
Une des difficultés rencontrée pour le traitement est que cette enquête provenait de deux sources différentes : questionnaires remplis sur internet, pour lesquels les jeunes pouvaient choisir de remplir tout ou partie de l’enquête ; questionnaires papier administrés dans les écoles (public captif), où les jeunes ont dû tout remplir. Pour certains thèmes ayant rencontré moins de succès sur internet, les non-réponses sont donc plus nombreuses.
Les éléments suivants sont donc importants à prendre en compte.
Le corpus de référence
Lorsqu’on fait parler les chiffres, il est important de les référer à un corpus de référence fiable. Quelques éléments sont donc à vérifier.
Echantillon total et strates
L’échantillon total comprend tous les questionnaires rentrés, soit ici 908 questionnaires, correspondant à 908 jeunes. Chose rarissime, il y a autant de filles que de garçons.
La strate est la partie de l’échantillon total qui concerne une catégorie de jeunes (par exemple uniquement les filles, ou les jeunes qui vivent en famille recomposée, ou uniquement les jeunes qui brossent l’école, etc.), ou encore un groupe ciblé caractérisé par sa réponse (ex. les jeunes ayant répondu « oui » à telle question).
Travailler par strate permet d’affiner les réponses d’un groupe précis. Les pourcentages calculés par strates ne correspondent plus à l’échantillon total, mais à l’échantillon de la strate, c’est-à-dire que le nombre de jeunes est chaque fois différent en fonction de la strate.
Cela permet aussi de compenser le problème décrit plus haut, en réduisant le nombre de non-réponses dû au fait que des jeunes, dans la version internet, ont « zappé » des parties entières du questionnaire.
Dans certains cas, les résultats auront intérêt à être présentés au départ de l’échantillon total (pour les parties obligatoires, même sur internet) ; dans d’autres cas, il vaut mieux travailler par strates.
Mais il est essentiel de l’indiquer très clairement dans le rapport, sans quoi le lecteur peut prendre la partie pour le tout ! Et lorsque l’AMO est lectrice de chiffres qu’elle n’a pas produits, il importe de vérifier quelle est la base de calcul choisie par l’opérateur.
Observations et citations
Le nombre d’observations correspond au nombre de répondants, donc ici, au nombre de jeunes.
L’échantillon total comprend donc 908 observations. La strate « filles » comprend 454 observations, etc.
Les citations sont le nombre d’items cochés par les répondants dans une question.
Dans les cas où une seule réponse est possible, les nombres d’observations et de citations coïncident. Dans le cas de réponses multiples, les citations sont plus nombreuses que les observations.
Pourcentages selon les observations ou les citations
Les pourcentages peuvent être calculés soit par rapport aux observations, soit par rapport aux citations.
- Dans le cas des pourcentages selon les observations, le calcul est fait par rapport au nombre de répondants (soit par rapport au nombre de jeunes dans l’échantillon total ou dans la strate choisie).
- Dans le cas des pourcentages selon les citations, le calcul se fait par rapport au nombre de réponses (soit, dans le cas de réponses multiples, avec plus de réponses que de répondants).
Le choix n’est pas indifférent.
Avec les pourcentages par observations, on cherche à savoir le nombre de jeunes qui ont donné telle réponse. Avec le nombre de citations, on cherche, parmi les réponses multiples, quelle est la part relative de chaque réponse.
Les pourcentages peuvent donc être très différents et il convient de ne pas confondre l’objectif.
Prenons un exemple
Soit la question : « En cas de problèmes, vers qui te tournes-tu ? », qui comportait 9 réponses possibles. Les jeunes pouvaient donner plusieurs réponses. Parmi ces réponses, il y a « Je me tourne vers un ami ».
Si on regarde le pourcentage par observations, sur les 908 jeunes de l’échantillon total, 61,3 % (soit 557 jeunes) disent se tourner vers un ami. Donc, pour 6 jeunes sur 10, l’ami est un confident. Cela veut dire qu’il y a néanmoins 4 jeunes qui ne se tournent pas vers un ami en cas de problème. Ce qu’on calcule ici, c’est la proportion de jeunes qui choisissent ou non cet item.
Mais c’était une question à réponses multiples, ce qui veut dire que certains jeunes ont donné une seule réponse, mais que d’autres en ont donné 2, 3, 4… ou plus encore, puisqu’il y en avait 9 possibles. Ils se tournent vers plusieurs personnes. Pour les 908 jeunes, il y a eu 1626 réponses pointées en tout. Si on calcule le pourcentage au départ de ces 1626 réponses, on obtient un pourcentage par citations. La réponse « Je me tourne vers un ami » voit dès lors son score diminuer, puisqu’elle ne représente plus que 34,3 % de l’ensemble des réponses.
Est-ce pour autant que le recours aux amis a diminué ? Pas du tout, il y a toujours 557 jeunes qui le citent. Simplement, ici, ce qu’on calcule, c’est la « part du gâteau » qui est remportée par les amis dans l’ensemble des solutions possibles.
Donc, si on dit ici que « 34,3 % des jeunes se tournent vers un ami », c’est faux (ils sont 61,3 % à le faire) ! Ce qu’il faut dire, c’est « Dans l’ensemble des solutions cumulées possibles pour les jeunes, les amis comptent pour une part de 34,3 % ».
Et ce mode de calcul, par contre, ne dit rien de la proportion de jeunes qui ne se tournent pas vers un ami en cas de difficulté, contrairement au premier.
Les deux méthodes donnent donc des résultats différents, mais qui ont chacun leur intérêt. Ainsi, le pourcentage par observations pour cette question précise dit objectivement la proportion de jeunes qui a recours ou non à la solution « amis ». Il peut être intéressant de creuser pourquoi 40 % ne se tournent jamais vers un ami. Y a-t-il une faiblesse particulière à propos du réseau autour de ces jeunes, pour laquelle une action d’AMO pourrait être utile ? Il pourrait être intéressant de faire une recherche sur cette strate de 40 % : quel profil ont-il, quel âge, filles ou garçons, vivant dans quelle région, avec quels types de difficultés pointées par ailleurs etc.
Pourcentages au total, en lignes ou en colonnes
La lecture des tableaux statistiques se complique lorsqu’on est devant des tableaux croisés.
Prenons l’exemple d’une enquête d’une AMO sur le rapport des jeunes à l’alcool. L’enquête a été administrée dans le cadre d’écoles secondaires. 631 jeunes de 12 à 17 ans ont répondu à la question « As-tu déjà consommé un verre de boisson alcoolisée ? » (284 filles et 347 garçons).
Pour comparer les pratiques des filles et des garçons, on a eu recours à des croisements. Trois types de résultats croisés peuvent être présentés sous forme de tableau.
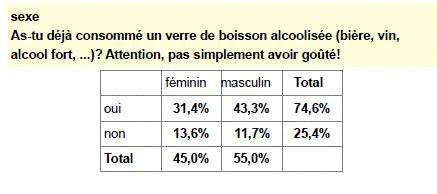
- Les pourcentages au total sont calculés sur l’échantillon total. Les pourcentages qui apparaîtront dans chaque case sont donc la fraction de l’échantillon total qui correspond à la case croisée en question : dans cette case sont répertoriés x % de l’échantillon total.
Dans l’échantillon total concernant les jeunes et l’alcool, la répartition est donc la suivante ; 31,4 % de filles ayant déjà bu, 13,6 % n’ayant jamais bu ; 43,3 % de garçons ayant déjà bu, 11,7 % n’ayant jamais bu. L’addition de tous ces pourcentages est de 100 %, c’est ce qui permet aussi de repérer qu’il s’agit de pourcentages au total.
- Les pourcentages en lignes ou en colonnes sont calculés sur des strates qui sont juxtaposées ans un tableau.
-
-
-
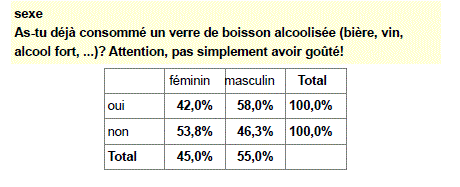
Les pourcentages en lignes doivent être lus en lignes, ils sont calculés sur 100 % de chaque strate/ligne et uniquement sur cette base.
Voici ci-dessous les pourcentages en lignes du tableau précédent ; le total 100 % est en bout de lignes. Il faut lire le tableau horizontalement : les jeunes qui ont répondu « oui » (donc la strate de ceux qui ont déjà bu) sont à 42 % des filles et à 58 % des garçons. Ceux qui ont répondu « non » – les non-buveurs, donc – sont à 53,8 % des filles et à 46,3 % des garçons.
-
-
-
-
-
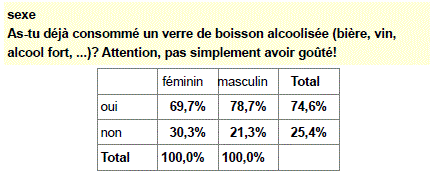
Les pourcentages en colonnes doivent être lus en colonnes, ils sont calculés sur 100 % de chaque strate/colonne et uniquement sur cette base.
Voici ci-dessous les pourcentages en colonnes du même tableau : le total 100 % se trouve en bas des colonnes, il faut donc lire le tableau verticalement.
Dans la strate des filles, 69,7 % ont déjà bu, 30,3 % jamais. Dans celle des garçons, 78,7 % ont déjà bu, 21,3 % jamais.
-
-
Pas question, donc, de lire en colonnes des pourcentages qui sont faits pour être lus en lignes. Pour éviter la confusion, il faut regarder où se trouve le total « 100 % ». Si c’est à droite du tableau, au bout des lignes, c’est qu’il s’agit de pourcentages en lignes. Si c’est sous le tableau, c’est qu’il s’agit de pourcentages en colonnes.
Autre indice : quand il est visible que l’addition de tous ces pourcentages dépasse 100 %, c’est qu’il ne s’agit en aucun cas de pourcentages au total.
Tous les modes de lecture ne sont pas pertinents, selon ce qu’on cherche à savoir. Dans ce cas-ci, si on veut comparer les pratiques des filles et celles des garçons, ce sont les pourcentages en colonnes qui sont les plus pertinents, car ils permettent des comparaisons qui ne sont pas biaisées : il y a moins de filles que de garçons dans l’échantillon total, il est donc logique de faire le calcul strate de genre par strate de genre : le pourcentage sera calculé par rapport à la population de cette strate, et on pourra comparer les usages selon le genre : les garçons sont proportionnellement plus nombreux que les filles à avoir déjà bu de l’alcool.
Mode, moyenne, médiane
Le mode est la valeur ou la modalité dont l’effectif est le plus élevé. En d’autres termes, c’est la réponse qui est la plus fréquemment citée.
La moyenne arithmétique est la somme des valeurs de la variable divisée par le nombre d’individus.
La médiane est un nombre qui divise en 2 parties égales la population telle que chaque partie contient le même nombre de valeurs : il y a autant de personnes d’un côté ou de l’autre du point médian.
Chaque type de calcul a son utilité, mais encore une fois il faut être attentif. Par exemple, dans le cas de la moyenne, les valeurs extrêmes (les plus grandes et les plus petites) peuvent déformer les résultats. Par exemple, si on calcule la moyenne des salaires dans une commune, s’il y a un milliardaire parmi les répondants, le calcul sera totalement faussé. Il vaut mieux, alors, utiliser la médiane.
Exemple
Soit un groupe de 8 jeunes de 12 à 18 ans, se composant comme suit :
12, 13, 13, 15, 16, 17, 17, 17 ans.
Le mode est 17 ans (valeur la plus citée)
La moyenne est 12+13+13+15+16+17+17+17 : 8 = 120 : 8 = 15 ans (addition de toutes les données, divisée ensuite par le nombre de répondants)
La médiane, qui coupe le groupe exactement en 2, est entre 15 et 16, soit 15,5 ans.
POUR EN SAVOIR PLUS *La série « la statistique expliquée à mon chat » sur YouTube aborde des notions statistiques complexes de manières ludique et pédagogique. https://www.youtube.com/channel/UCWty1tzwZW_ZNSp5GVGteaA *Par exemple, pour comprendre la différence entre la moyenne et la médiane: https://www.youtube.com/watch?v=uIx2xvdwIIo *Ou encore, pour comparer le calcul de la moyenne, de la médiane et du mode : https://fr.khanacademy.org/math/probability/data-distributions-a1/summarizing-center-distributions/v/mean-median-and-mode